Rockm3'Blog

petgraph简明教程

发表于 2024-09-30 更新于 2024-10-01 分类于 Rust 本文字数： 2.4k 阅读时长 ≈ 9 分钟

logo

1. 简介

Rust中用于图数据结构处理的库，可以处理与图数据结构相关的各种算法。支持无/有向图、稳定图、带权图等。值得一提的是，Petgraph支持树，但是并没有单独设计树的数据结构。

2. 图的类型和简例

2.1 `Graph`通用图

图的基础结构体，其他部分结构体由Graph派生。Graph背后的内存模型是邻接表，其对节点和边的类型无任何限制。

其定义为：

pub struct Graph<N, E, Ty = Directed, Ix = DefaultIx> {  
    nodes: Vec<Node<N, Ix>>,  
    edges: Vec<Edge<E, Ix>>,  
    ty: PhantomData<Ty>,  
}

节点关联数据 N 和边关联数据 E,称为权重。关联数据可以是任意类型。

边类型 Ty,用于确定图边是有向图还是无向图。其中Directed为有向图，Undirected为无向图。

Ix为索引类型，默认u32。

创建一个通用无向图：

1	let mut graph: Graph<&str, i32, Undirected> = Graph::new_undirected();

添加一些示范节点：

// 添加12个节点  
let node_names: [&str; 12] = [  
    "Node1", "Node2", "Node3", "Node4", "Node5", "Node6",  
    "Node7", "Node8", "Node9", "Node10", "Node11", "Node12",  
];  
  
// 用一个向量来存储节点的索引  
let mut nodes: Vec<NodeIndex<u32>> = Vec::new();  
  
// 添加节点到图中  
for &name in &node_names {  
    let node: NodeIndex<u32> = graph.add_node(name);  
    nodes.push(node);  
}

在图中添加一些分支：

// 定义边的连接信息和权重  
let edges: [(usize, usize, u32); 14] = [  
    (0, 1, 5),  
    (0, 2, 10),  
    (0, 3, 7),  
    (1, 4, 3),  
    (1, 5, 6),  
    (2, 6, 8),  
    (3, 7, 12),  
    (3, 8, 11),  
    (4, 9, 4),  
    (5, 10, 9),  
    (6, 11, 14),  
    (7, 8, 15),  
    (9, 10, 2),  
    (10, 11, 1),  
];  
  
// 从数组中加载边并添加到图中  
for &(source, target, weight) in &edges {  
    graph.add_edge(nodes[source], nodes[target], weight as i32);  
}

其结果如下图所示：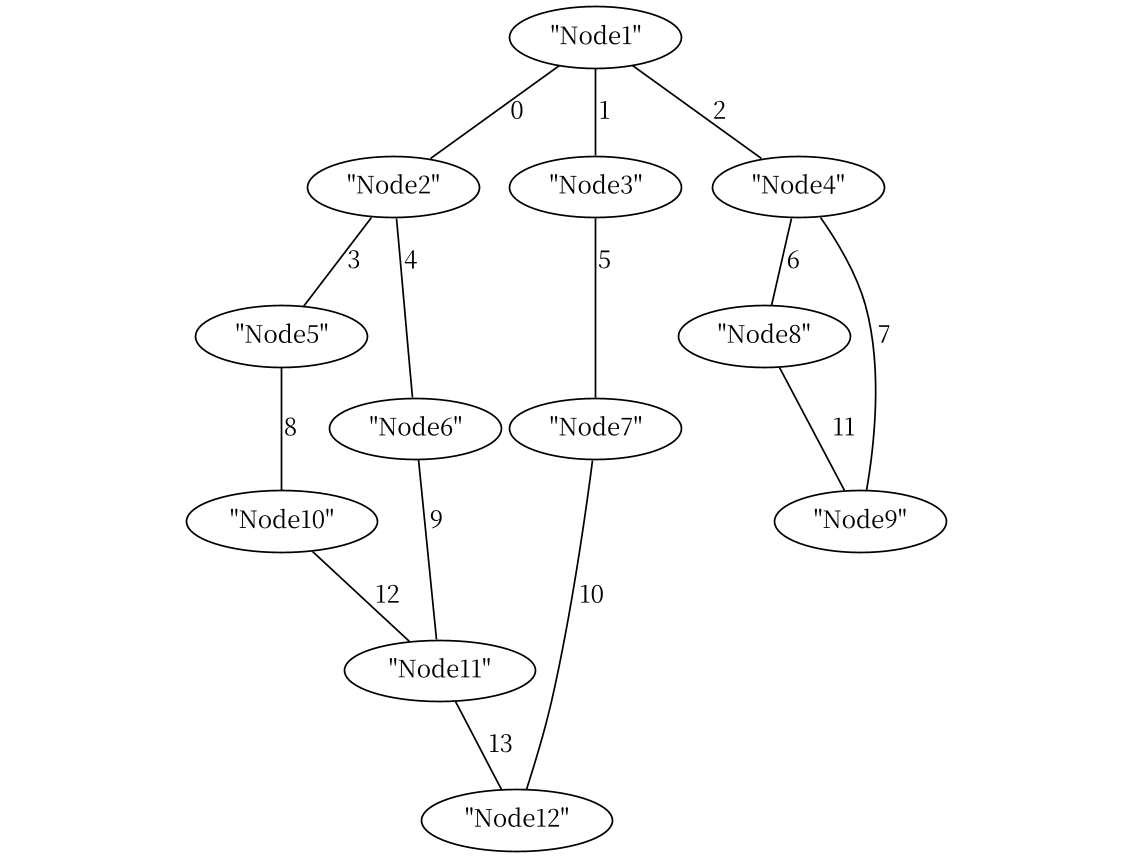

可以安装一个dot文件预览插件，可以帮助我们更好的处理图的结构。
使用下面的代码导出文件为dot文件。

1
2
3

let dot_output = Dot::with_config(&graph, &[Config::EdgeIndexLabel]);  
let mut file1 = File::create("graph.dot").expect("Unable to create file");  
write!(file1, "{:?}", dot_output).expect("Unable to write data");

完整代码如：

use std::fs::File;  
use petgraph::dot::{Config, Dot};  
use petgraph::graph::{Graph, NodeIndex};  
use petgraph::Undirected;  
use std::io::Write;  
fn main() {  
    // 创建一个通用的无向图  
    let mut graph: Graph<&str, i32, Undirected, u32> = Graph::new_undirected();  
  
    // 添加12个节点  
    let node_names: [&str; 12] = [  
        "Node1", "Node2", "Node3", "Node4", "Node5", "Node6",  
        "Node7", "Node8", "Node9", "Node10", "Node11", "Node12",  
    ];  
  
    // 用一个向量来存储节点的索引  
    let mut nodes: Vec<NodeIndex<u32>> = Vec::new();  
  
    // 添加节点到图中  
    for &name in &node_names {  
        let node: NodeIndex<u32> = graph.add_node(name);  
        nodes.push(node);  
    }  
  
    // 定义边的连接信息和权重  
    let edges: [(usize, usize, u32); 14] = [  
        (0, 1, 5),  
        (0, 2, 10),  
        (0, 3, 7),  
        (1, 4, 3),  
        (1, 5, 6),  
        (2, 6, 8),  
        (3, 7, 12),  
        (3, 8, 11),  
        (4, 9, 4),  
        (5, 10, 9),  
        (6, 11, 14),  
        (7, 8, 15),  
        (9, 10, 2),  
        (10, 11, 1),  
    ];  
  
    // 从数组中加载边并添加到图中  
    for &(source, target, weight) in &edges {  
        graph.add_edge(nodes[source], nodes[target], weight as i32);  
    }  
    
    let dot_output = Dot::with_config(&graph, &[Config::EdgeIndexLabel]);  
    let mut file1 = File::create("graph.dot").expect("Unable to create file");  
    write!(file1, "{:?}", dot_output).expect("Unable to write data");  
}

2.2 `DiGraph`有向图

有向图DiGraph派生于Graph，与Graph大同小异，其定义如下：

1	pub type DiGraph<N, E, Ix = DefaultIx> = Graph<N, E, Directed, Ix>;

具体有向图的创建不再赘述，只给出实例化代码：

1	let mut graph: DiGraph<&str, i32, u32> = DiGraph::new();

其结果输出为：

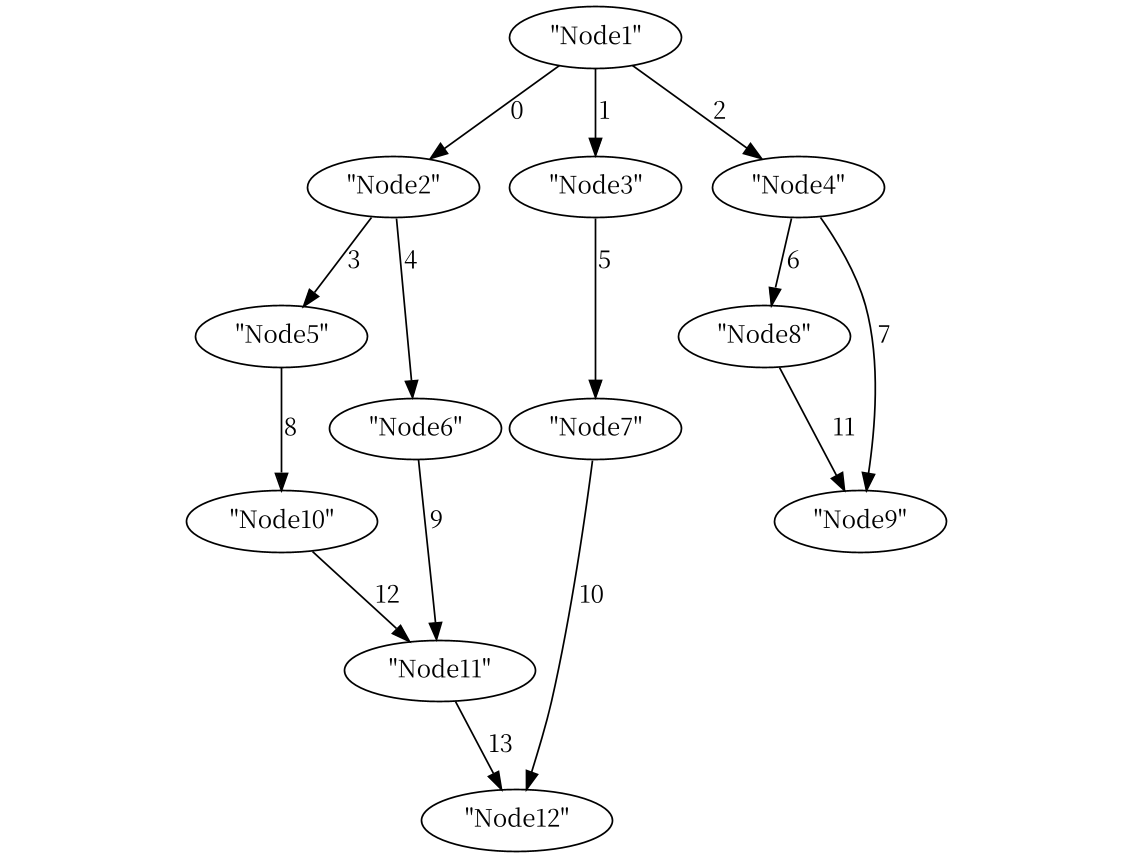
2.3 `UnGraph`无向图

同理，不在赘述。

2.4 `StableGraph`稳定图

与Graph类似，StableGraph背后的内存模型也是邻接表。删除节点或者分支时，不会改变其他节点或者分支的索引。其特性更适合频繁增添/删除边的逻辑算法，例如：生成树的构建、割集的计算、基本回路的计算等等。

其定义如下：

pub struct StableGraph<N, E, Ty = Directed, Ix = DefaultIx> {  
    g: Graph<Option<N>, Option<E>, Ty, Ix>,  
    node_count: usize,  
    edge_count: usize,  
    free_edge: EdgeIndex<Ix>,  
}

同样，对于StableGraph，也有有向图和无向图的相应派生：

pub type StableDiGraph<N, E, Ix = DefaultIx> = StableGraph<N, E, Directed, Ix>;
pub type StableUnGraph<N, E, Ix = DefaultIx> = StableGraph<N, E, Undirected, Ix>;

3. 算法

3.1 最小生成树算法

pub fn min_spanning_tree<G>(g: G) -> MinSpanningTree<G>  
where  
    G::NodeWeight: Clone,  
    G::EdgeWeight: Clone + PartialOrd,  
    G: IntoNodeReferences + IntoEdgeReferences + NodeIndexable,

计算图的最小生成树。输入图被视为无向图。使用Kruskal算法。实际上返回的是最小生成森林,即图每个连通分量的一个最小生成树。

示例代码：

let mst = min_spanning_tree(&graph);  
let mut tree: DiGraph<&str, i32, u32> = DiGraph::new();  
for &name in &node_names {  
    tree.add_node(name);  
}
  
for element in mst {  
    // 解构 Element::Edge
	if let Element::Edge { source, target, weight } = element {  
        let source_index = NodeIndex::new(source);  
        let target_index = NodeIndex::new(target);  
        tree.add_edge(source_index, target_index, 0);  
    }  
}

其输出结果如下：

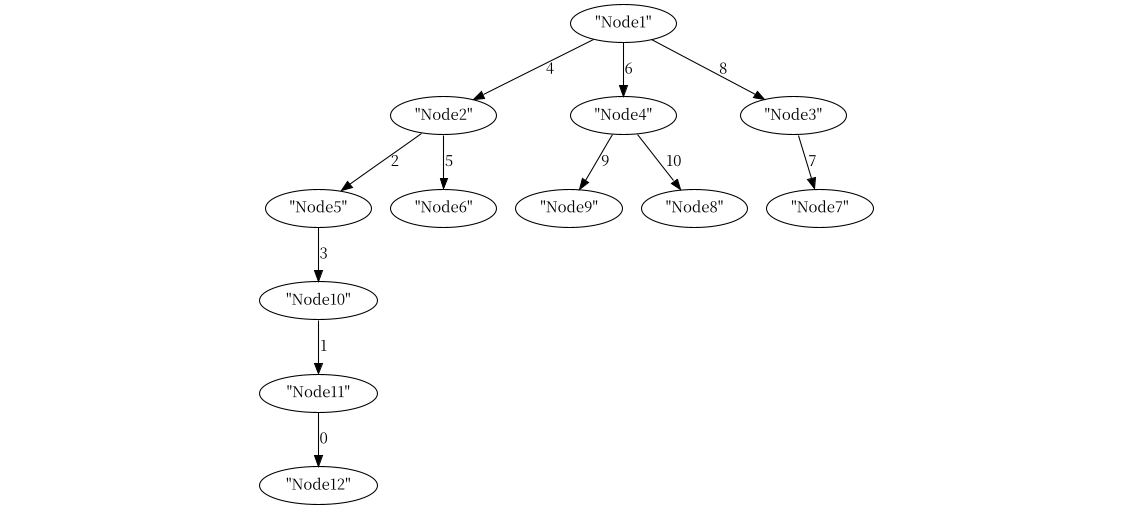
输出结果不同？这是由于tree.add_node(name);添加节点时改变了节点索引。所以在进行最小生成树生成时最好对原图节点和分支进行clone，并使用StableGraph去掉连枝，以维持稳定性（如果需要的话）。也可以选择只clone节点，但是生成树的分支索引都是不可信的。

3.2 最短路径算法

Petgraph实现的最短路径算法有dijkstra算法、astar算法和BellmanFord算法等等。其中，dijkstra算法并不返回路径，而是返回一个Map，它包含了起始节点到每一个可达节点的最短路径成本。BellmanFord算法使dijkstra算法支持负权重。

我使用astar算法求解最短路径。

其实现代码如下：

let result = astar(  
    &tree,  
    *source_index,  // 起始节点  
    |finish| finish == *target_index,  // 目标节点  
    |e| *e.weight(),  // 边权重  
    |_| 0,  // 启发函数，在此简单设置为 0
);
// 输出路径  
if let Some((_cost, path)) = result { ... }

其路径path是路径节点的索引集合。

3.3 强连通分量

Petgraph使用Kosaraju算法计算强连通分量。对于无向图来说，计算的就是连通分量。通过迭代计算，对节点进行两次遍历。

其实现代码如下：

let scc = kosaraju_scc(&tree);  
for (i, group) in scc.iter().enumerate() {  
    println!("Group {} {:?}:", i, group);  
}

其中，每一个Group都是一个连通分量，是连通分量节点的索引集合。

3.4 遍历算法

3.4.1 深度优先算法`DFS`

深度优先需要用到petgraph::visit::Dfs，其简单实现如下：

use petgraph::visit::Dfs;

let mut dfs_graph = Graph::<(),(), petgraph::Undirected>::new_undirected();

//      0
//     /|\
//    1 2 3
//        |
//        4
dfs_graph.extend_with_edges(&[
    (0, 1), (0, 2), (0, 3), (3, 4)
]);

for start in dfs_graph.node_indices() {
    let mut dfs = Dfs::new(&dfs_graph, start);
    
    print!("[{}] ", start.index());
    
    while let Some(visited) = dfs.next(&dfs_graph) {
        print!(" {}", visited.index());
    }
    println!();
};

输出结果为：

[0]  0 1 2 3 4
[1]  1 0 2 3 4
[2]  2 0 1 3 4
[3]  3 0 1 2 4
[4]  4 3 0 1 2

3.4.2 广度优先算法`BFS`

广度优先需要用到petgraph::visit::Bfs，用法跟广度优先一样，只需要将Dfs替换成Bfs即可，其实现如下：

use petgraph::visit::Bfs;

let mut bfs_graph = Graph::<(),(), petgraph::Undirected>::new_undirected();

//      0
//     /|\
//    1 2 3
//        |
//        4
bfs_graph.extend_with_edges(&[
    (0, 1), (0, 2), (0, 3), (3, 4)
]);


for start in bfs_graph.node_indices() {
    let mut bfs = Bfs::new(&bfs_graph, start);
    
    print!("[{}] ", start.index());
    
    while let Some(visited) = bfs.next(&bfs_graph) {
        print!(" {}", visited.index());
    }
    
    println!();
};

输出结果为：

[0]  0 3 2 1 4
[1]  1 0 3 2 4
[2]  2 0 3 1 4
[3]  3 4 0 2 1
[4]  4 3 0 2 1

3.4.3 后序深度优先算法`DfsPostOrder`

有时我们可能需要先迭代节点的邻居，然后是节点本身。petgraph为这种遍历顺序提供了DfsPostOrder。使用方式与深度遍历相同：

use petgraph::visit::DfsPostOrder;

let mut dfs_graph = Graph::<(),(), petgraph::Undirected>::new_undirected();

//      0
//     /|\
//    1 2 3
//        |
//        4
dfs_graph.extend_with_edges(&[
    (0, 1), (0, 2), (0, 3), (3, 4)
]);


for start in dfs_graph.node_indices() {
    let mut dfs = DfsPostOrder::new(&dfs_graph, start);
    
    print!("[{}] ", start.index());
    
    while let Some(visited) = dfs.next(&dfs_graph) {
        print!(" {}", visited.index());
    }
    
    println!();
};

输出结果为：

[0]  1 2 4 3 0
[1]  2 4 3 0 1
[2]  1 4 3 0 2
[3]  1 2 0 4 3
[4]  1 2 0 3 4

3.5 其他算法

除了寻路算法，petgraph还有很多其他算法，这里简单列举一些常用的算法：

all_simple_paths：返回给定节点上所有路径的迭代器。
condensation：将每个强连接节点归并到一个节点。
connected_components：返回连通节点数。
has_path_connecting：如果两个节点间存在连通路径则返回True。
is_cyclic_directed：如果图中包含至少一个有向环则返回True。
is_cyclic_undirected：如果图中包含至少一个环则返回。
tarjan_scc：用 Tarjan 算法返回强连通分量向量。
dominators：实现支配节点算法，用于计算图中某个节点的支配节点，通常应用于编译器分析和控制流图。
feedback_arc_set：实现反馈弧集算法，用于找到并移除最少数量的边，使得图中没有循环（在有向图中应用）。
floyd_warshall：实现Floyd-Warshall算法，用于计算图中所有节点对的最短路径，适用于稠密图（即边数量较多的图）。
ford_fulkerson：实现Ford-Fulkerson算法，用于解决最大流问题，通过增广路径寻找图中的最大流量。
isomorphism：实现同构算法，用于检测两个图是否是同构的（即结构上相同）。
k_shortest_path：实现K-最短路径算法，用于寻找图中从源节点到目标节点的K条最短路径。
matching：实现匹配算法，用于在图中寻找最大匹配或完美匹配，广泛应用于图的二分图匹配问题。
page_rank：实现PageRank算法，用于对图中的节点进行排序，最初由谷歌提出，用于网页排名。
simple_paths：提供与简单路径相关的算法，例如寻找图中两点之间的所有简单路径（不重复经过同一个节点的路径）。
tred：实现拓扑排序算法，用于对有向无环图（DAG）中的节点进行线性排序，广泛用于依赖关系解析、任务调度等场景。

petgraph并没有实现寻找回路的算法，可以拆解为寻找路径的算法曲线实现。

4. 参考文献

[1] Jarodyv. (2023, February 21). Rust机器学习之petgraph. CSDN. https://blog.csdn.net/jarodyv/article/details/128796914
[2] Petgraph Developers. (2024). Petgraph library for Rust. GitHub. https://github.com/petgraph/petgraph

1. 简介

2. 图的类型和简例

2.1 Graph通用图

2.2 DiGraph有向图

2.3 UnGraph无向图

2.4 StableGraph稳定图

3. 算法

3.1 最小生成树算法

3.2 最短路径算法

3.3 强连通分量

3.4 遍历算法

3.4.1 深度优先算法DFS

3.4.2 广度优先算法BFS

3.4.3 后序深度优先算法DfsPostOrder

3.5 其他算法

4. 参考文献

2.1 `Graph`通用图

2.2 `DiGraph`有向图

2.3 `UnGraph`无向图

2.4 `StableGraph`稳定图

3.4.1 深度优先算法`DFS`

3.4.2 广度优先算法`BFS`

3.4.3 后序深度优先算法`DfsPostOrder`